The Discovery and Beauty of Quaternions

👋 Hey Friends,
Welcome back to a new episode of the Sunday Night Sky, the newsletter where we explore and learn about new scientific achievements and astrophysical, mathematical, and physical theories to understand the world around us a little better.
Today we want to dive into the world of four-dimensional numbers, known as quaternions. Thanks for reading today's episode. :)

Are there any numbers beyond the complex numbers?
Back in the year 1840 a mathematician, named William Rowan Hamilton, tried to solve a tenacious problem. He was aware of the 2D-dimensional number system, known as complex numbers which is a numerical system where a so-called complex number can be represented as a point on a 2D-Plane, as such.

This story today is a story of an obsession with abstract numbers and how they turned out to help solve real-world problems. The discovery helped solve problems so relevant, that we use them frequently today!
The Discovery
We picture the year 1843 when Hamilton was already obsessively solving difficult problems for quite some time. His biggest obsession by far was regarding the development of a number system which lies beyond two dimensions, like complex numbers. As it was already well known by then you are able to represent a point in 3D space by a coordinate triple of \( \ (x,y,z)\). For Hamilton, this was well understood, including the vectorial addition of these coordinate triples. But the problematic part was that he wasn't able to find an appropriate formulation for multiplication.
The following is a letter that Hamilton wrote later to his son Archibald:
Every morning in the early part of October 1843, on my coming down to breakfast, your brother William Edwin and yourself used to ask me: “Well, Papa, can you multiply triples?” Whereto I was always obliged to reply, with a sad shake of the head, “No, I can only add and subtract them.”
While walking across the Brougham Bridge in Dublin he had a general realization that he couldn't formulate a successful rule for multiplication in three dimensions but in four dimensions instead. By using three of the numbers in the quadruple (a point in 4-dimensional space) as the points of a coordinate in 3D space, Hamilton could represent points in space by his new system of numbers but they had to extend into the fourth dimension for the algebra to work out. This was his great insight!
Actually, he was so amazed by his discovery, that, in his quick mathematical fear that the theory could be lost at any moment (after all, you could die each second), he carved the basic rules for multiplication into the stones of the bridge:
\( \ i² = j² = k² = ijk = −1.\)
On the following day, Hamilton wrote a letter to his friend and fellow mathematician, John T. Graves, describing the miracle on the bridge.
“And here there dawned on me the notion that we must admit, in some sense, a fourth dimension of space for the purpose of calculating with triples … An electric circuit seemed to close, and a spark flashed forth.”
Hamilton called a quadruple with these rules of multiplication a quaternion, and he devoted the remainder of his life to studying and teaching them. And so he did.
The Mathematics behind quaternions
Quaternions as confusing and mystical as they seem, are actually not that far away from the general idea of complex numbers since in the system of quadruples we also find an algebraic and geometric representation. Actually, the field of complex numbers is in some sense embedded inside the space of quaternions so we, as the people who try to understand Hamilton's life work, should in fact expect that we can find some general formulation for basic algebraic operations and more. As we will see, this is indeed true!
So we have a chain of sets ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ ⊂ ℂ ⊂ ℍ where each set is a subset of the set on the right. These sets are natural numbers, integers, rational numbers, real numbers, complex numbers, and quaternions respectively. A natural question is then:
Can we expand this numerical system to even higher dimensional numbers than quaternions?
The answer to this question is “yes”, but we need to learn how to walk before we try to run, so let’s talk about the quaternions first! (Maybe we explore some of the others in the following weeks. :) )
Just as we can view a complex number as a point (and a vector) in ℝ² (2-dimensional space over the real numbers), we can view quaternions as points in ℝ⁴, and therefore we need 4 real numbers to define a quaternion. This makes the expression for quaternions relatively "easy":
\( \ q =a + bi + cj + dk\)
\( \ a, b, c, d\) are just real numbers. Analogous to this you can think of \( \ a, b, c, d\) as somewhat the components of four-dimensional vectors where each component stretches or squeezes in a certain dimension:

Specifically, we have i² = j² = k² = ikj = -1 (which was what Hamilton wrote down on the bridge), and moreover,
- ij = k,
- ji = -k,
- jk = i,
- kj = -i,
- ki = j,
- ik = -j.
Together with the distributive law and the associative law which also holds for quaternions, these rules define the algebra of ℍ.
Note that quaternions are not commutative. That is, in general, qw ≠ wq. This might seem strange at first that we need to keep track of the direction we multiply numbers together, but those of you who have been dragged through endless hours of linear algebra know that many other mathematical structures and spaces share this non-commutativity property.
In some cases, a quaternion can be expressed as the sum of a scalar part a and a vector part v. This can be written as q = a + bi + cj + dk = a + v, where v = bi + cj + dk.
In this form, the conjugate of a quaternion can be expressed as q = a - v = a - bi - cj - dk*. The norm of a quaternion is the square root of the product of the quaternion and its conjugate. It represents the distance from the origin to the quaternion in ℝ⁴. Specifically,
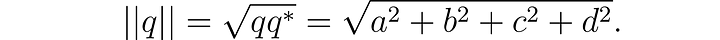
This is effectively Pythagoras’ theorem in four dimensions.
Euler discovered a remarkable relationship between the exponential function and the trigonometric functions through the complex number i. Specifically,
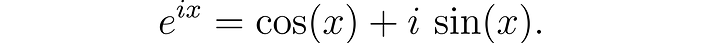
One of the attractive features of quaternion theory is the Euler formula for quaternions. It states that if we write a quaternion q = a + v, the following elegant relationship holds:
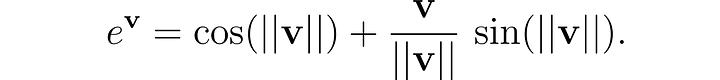
We should note that this is a generalization of Euler’s formula since the two formulas coincide when we have a quaternion z = xi where a = c = d = 0.
Hamilton introduced quaternions as a means of working with rotations in three-dimensional space. Despite living in four dimensions, they prove to be highly effective in this context if we only consider the vector part, which resides in ℝ³.
This makes quaternions an incredibly interesting numerical system to study and we are far beyond knowing everything about 4,5,6 or even n-dimensional number systems.
If you have enjoyed this episode of THE SUNDAY NIGHT SKY and you don't want to miss out on any future episodes consider subscribing for FREE.
Thanks again and I'll see you soon.
xoxo
Victor 👋 :) (@observethecosmos)
🎥 Youtube Video
The world of complex analysis: Complex Numbers
Embark on a fascinating journey through the depths of Complex Analysis. Get ready to uncover the hidden secrets of complex functions, understand the power of holomorphic functions, and broaden your mathematical knowledge. Join me and explore the beauty, elegance, and utility of Complex Analysis, and gain new insights into mathematics and its applications. This first episode covers most of the basics but be ready to dive into the details very soon...
✍️ Quote of the week
🎟 Want to advertise on The Sunday Night Sky? → Send E-Mail
Check out some of my social media pages to learn more about math, science and astronomy:
🎬:Youtube